魔方作为一种经典的智力玩具,一直以来都是人们研究和挑战的对象。而针对数万阶魔方的复原问题,人们常常被其巨大的复杂性所困扰。然而,通过计算机算法的帮助,我们能够轻松地解决这个难题。
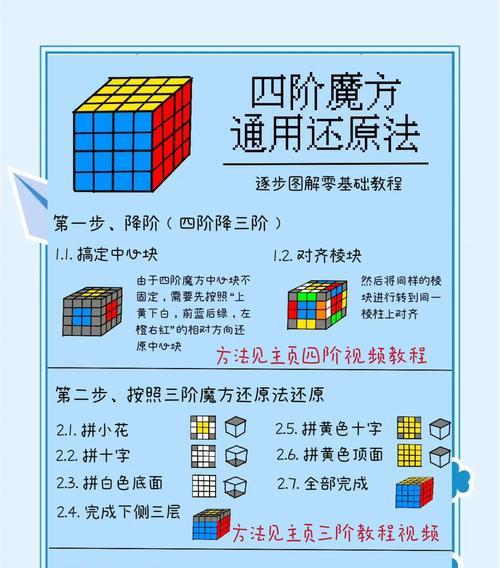
1.了解一万多阶魔方:介绍一万多阶魔方的概念和特点,让读者对这个超级复杂的魔方有一个初步认识。
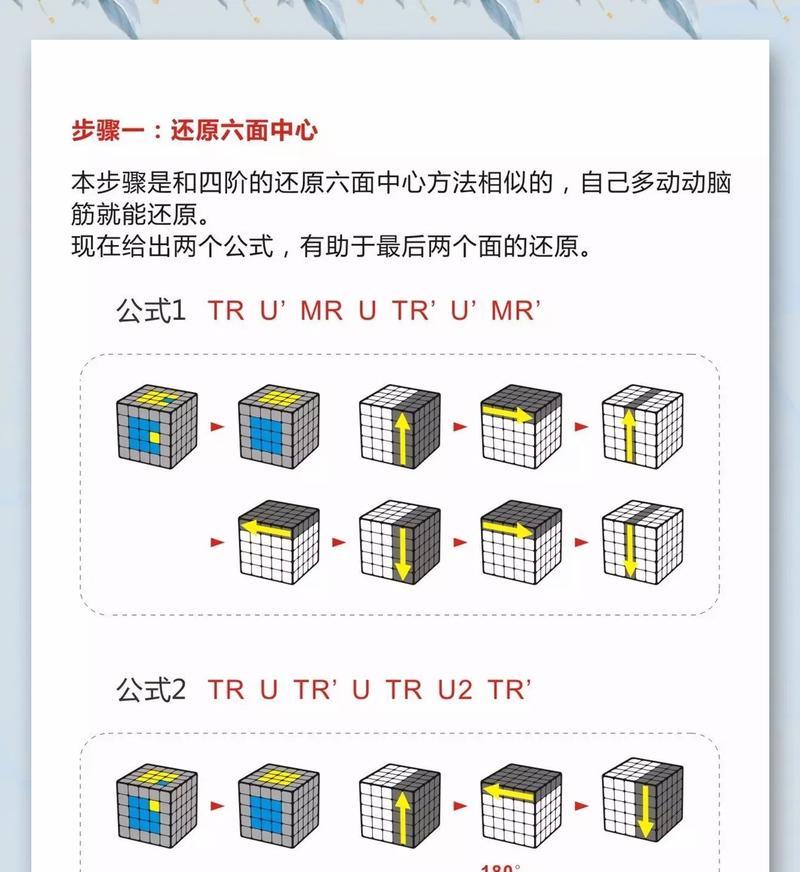
2.搜索并学习相关算法:介绍在计算机领域中用于解决魔方问题的算法,如弗里德里希(Fridrich)方法、Kociemba算法等,并说明它们的原理和应用。
3.开始准备:介绍解决一万多阶魔方所需的硬件和软件条件,如使用一台高性能计算机和相应的求解软件等。
4.设置输入参数:讲解如何根据实际情况设置魔方的状态和复原目标,以便计算机能够正确地进行求解。
5.运行求解程序:详细说明如何使用计算机求解软件,通过命令行或图形界面输入指令,启动计算机的复原过程。
6.算法分析与优化:解释计算机求解过程中所使用的算法是如何进行搜索、评估和剪枝的,并介绍一些对算法的优化策略。
7.计算机求解的时间与空间复杂度:探讨一万多阶魔方问题在计算机上求解时所需的时间和存储空间,并分析其复杂度。
8.精确还原与近似还原:介绍通过计算机求解得到的解法是精确还原魔方还是近似还原魔方,以及它们之间的差异。
9.理解计算机求解过程中的局限性:分析计算机求解魔方问题所面临的局限性,如在某些特殊情况下可能无法找到最优解等。
10.优化计算机求解过程:提供一些优化计算机求解过程的方法,如使用多线程、并行计算、分布式计算等,以加快求解速度。
11.多次求解与统计分析:介绍如何进行多次求解,以验证计算机求解的可行性和稳定性,并通过统计分析得出求解的平均时间和成功率。
12.深入研究魔方理论:鼓励读者进一步研究魔方理论,了解更多高阶魔方的复原算法和技巧,挑战更高难度的魔方问题。
13.拓展应用:探讨计算机求解魔方问题的拓展应用,如在人工智能、图形学、密码学等领域的应用前景。
14.现实世界中的应用:介绍魔方问题在实际应用中的场景,如物流优化、路径规划、排班问题等,并说明计算机求解的价值和意义。
15.结语与展望:本文内容,强调通过计算机求解一万多阶魔方问题的重要性和可行性,并展望未来计算机算法在解决更复杂问题上的潜力。
通过计算机算法复原一万多阶魔方成为可能,为人们提供了更广阔的探索空间。通过理解和运用相关算法,调整输入参数,运行求解程序,优化求解过程,人们可以在电脑的帮助下轻松解决超级复杂的魔方问题。在这一过程中,我们对计算机算法的理解和优化也得到了提升,为其他领域的问题求解提供了新的思路和方法。未来,随着计算机算法的不断发展,我们相信更多复杂问题将会被成功解决。